INTRODUCTION
One concept that unites all therapeutic modalities including the surgical, medical, pharmacological, physiotherapeutic (as well as other health professions-related) and the psychological, is change; specifically the valid confirmation of an improvement in a patient’s health status due to intervention. This issue has been at the core of medicine and rehabilitation since their very inception as clinicians always aspired to treat successfully those in need of acute as well as chronic conditions. In fact, although the phrase “Primum non Nocere”–“First (Above All), Do No Harm”-was attributed to Thomas Sydenham, a 17th century prominent physician (1624–1689), (Smith, 2005). The Hippocratic Oath includes the promise “to abstain from doing harm”. Both attest to the fact that it is the moral/professional duty of the physician not to bring upon a negative change i.e. to worsen the health status of the patient.
WHAT IS CHANGE?
Indeed, what is change, in terms of either improvement or worsening (aggravation), is a complicated issue and, as this paper will indicate, involves clinical as well as statistical considerations. However change relates very intimately to the concept of difference i.e. change is judged based on a difference in some measurable entity and almost always it relates to a time span. For example, if a due to exercise rehabilitation, a patient with an arthroscopically reconstructed anterior cruciate ligament (ACL) increases his Lysholm score (Lysholm and Gillquist, 1982) from 61 to 72 within, say 2 weeks, this will be considered, prima faciae, a positive change. On the other and, if a patient is deemed to be moving his neck ‘better’ based on a visual inspection of his cervical movement, such a decision is qualitatively-based and hence the confirmation of a change is, at best, questionable. That said, in some instances the difference may be so dramatic that no measurement is actually necessary but in this paper, such changes are not the issue. Rather, the objective is to find out why change is not simple as it may seem to be and how is it applied at the level of individual patient / subject.
Why is the confirmation of change such a critical issue in rehabilitation? There are, in principle, two instances which mandate the estimation of change. One is during the intervention phase when a decision has to be made whether the patient has improved sufficiently to justify progressing from one regimen to another. For example, in many orthopedic cases, e.g. following shoulder ligamentous tears, the initial stage is the restitution of functional active range of motion. Once this is achieved progression (change), in the form of increased muscular exertion may follow, consisting initially of isometric contractions and then concentric contractions. Only after a functional concentric capacity has been achieved, adding eccentric activity may be indicated. Judging at what point in the rehabilitation process, such changes may be implemented, is a challenge for all parties involved.
The other instance relates to termination of rehabilitation i.e. when the patient is judged to have entered the treatment plateau at which no fundamental, functional or physiological change can be expected within reasonable medical probability in spite of continuing medical or rehabilitative procedures, the so-called maximal medical improvement (MMI). Here the absence of further change is the issue. In both instances, the treating clinician as well as the patient wish to have a well-based decision regarding the MMI. Moreover, rehabilitation, much like medicine, is a costly component in health economics. The insuring bodies, whether the government, public or private companies, insist nowadays on informed expenditure. In other words, therapeutic means/procedures that do not lead to proven changes should not be paid for. Therefore, the issue of efficiency depends at least partly in showing progress or proving MMI.
In its simplest form, change derives from the difference between the values of a specific outcome score taken over a time interval: T1 to T2 namely:
Straightforward examples may relate e.g. to blood pressure, body temperature, white blood cell count, ECG etc., but often the rate at which these differences s take place: Δ(OM)/ΔT (where OM – outcome measure) may be of importance. It should be borne in mind that as far as the typical medical tests are concerned, the tests are performed using very sensitive and accurate instruments, and almost always without the active cooperation of the patient. Moreover, modern testing systems and highly reliable test parameters are based on minimal involvement of the tester and thus his skill in performing the test is not a significant factor.
On the other hand, assessing rehabilitation outcomes depends strongly on measuring human performance, and as a result rehabilitation-related changes take on a drastically different dimension. In this case, the human factor, both of the patient/subject and that of the tester, is decisive. As far as the previous is concerned, the patient/subject is an integral part of the test and his full cooperation is a sine qua non condition for its validity. Sub-optimal cooperation in performing the test due to factors such as fatigue, motivation, intelligence, emotional status etc. have a direct effect on the test/assessment outcomes. As for the latter, the levels of skill and experience play their part. These background factors, which are largely absent from the abovementioned ordinary clinical tests introduce ‘noise’ into the measurement process namely the outcome scores include factors that are irrelevant to the measured entity and reflect temporary effects.
This situation has led to the acute need in accounting for these confounding factors which result in apparent but largely irrelevant effect on the scores of outcome measures. The solution was to analyze the reproducibility of the findings using a test-retest paradigm, where the ‘retest’ is undertaken under the same conditions of the ‘test’. What such paradigm yields is a measure of the consistency of the results. As a rule, the closer the results in the retest are to those obtained in the test, the higher the reproducibility and vice versa. Moreover, a high reproducibility means that the effect of the confounding factors is limited. Since with the lapse of time (normally days or weeks) some inevitable discrepancy between the test and retest scores occurs, no human performance-related parameter enjoys a perfect reproducibility. However, assuming equal conditions and ideal reproduction of the test scores, the analysis allows one to state with statistical confidence that based on a previous reproducibility study, whether a change (difference) in the scores reflects normal fluctuations (the confounding part) or that it is the result of intervention.
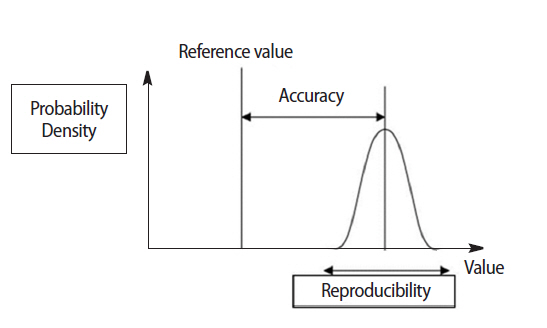
Thus in assessing change, irrespective of the measurement instrument (the most sophisticated or a simple questionnaire), two critical factors must be addressed: the reproducibility (consistency) and the accuracy of the measurement. As mentioned above, the reproducibility is the degree to which repeated measurements under unchanged conditions show the same results while the accuracy of a measurement is the degree of closeness of the measurement of a quantity to that quantity’s reference (true) value (Fig. 1). These two elements are independent, namely measurements may be accurate but not reproducible or vice versa, neither accurate nor reproducible or both. For example, if an experiment contains a systematic error, then increasing the sample size generally increases reproducibility but does not improve accuracy in the sense that the measurements fall away from the true value due to a flawed test or experiment. Eliminating the systematic error improves the accuracy without changing the reproducibility. In addition to accuracy and reproducibility, measurements are also characterized by their resolution (responsiveness) which is the smallest change in the underlying physical quantity that produces a response in the measurement. Measurement systems that successfully address all 3 characteristics at a high level are valid for clinical applications.
ACCURACY, REPRODUCIBILITY, AND RESOLUTION
To demonstrate the application of these concepts to real life situation consider the following question: In terms of accuracy, reproducibility and resolution, how do manual muscle testing, isometric and isokinetic, differ from each other in testing muscle strength?
Starting first with manual muscle testing (MMT), it should be borne in mind that this is a semi-quantitative measurement tool which is also highly nonlinear e.g. the difference between grade 1 and 2 is not equal for the difference between 4 and 5. If the strength of the subject or patient is above 3, it must be 4 or 5. Subdivisions into −4, 4, and 4+ have been made since the difference between grades 4 and 5 spans about 90% of the strength potential of the muscle (Dvir, 1997). However, this subdivision does not help in making the system more accurate and it even renders it less reproducible as the results of repeated tests do not zoom on the same value (e.g. 4+). Moreover, in terms of responsiveness MMT is specifically poor; increasing or decreasing the contraction level of the muscles does not necessarily lead to a change in the MMT grades unless the increase/decrease is at least 35% of the total force (Sapega, 1990). This all leads to a clinical assessment tool that is very poor in confirming change.
Using instrumented isometric testing in the form of a hand held dynamometer (HHD) is a decisive step forward. The reproducibility of HHD has been extensively studied and found to be satisfactory (Bohannon, 2012). This means that the test-retest results of isometric strength performed over days are sufficiently close to be clinically acceptable. These instruments are also quite accurate when correlated with other dynamometers but may suffer from bias, particularly when the tester himself is not strong enough. Moreover, HHDs are not suitable for e.g. trunk muscles testing, limiting their applicability. However HHDs are responsive namely, increase or decrease in the contraction output of the muscle can be traced with a resolution of ±1N.
Finally, isokinetic assessment of muscle strength is accurate, reproducible and responsive (Dvir, 2004) as long as the muscle torque exceeds that of the gravitational torque (when the plane of testing is anti-gravitational) which satisfies the basic requirements of clinical validity of a measurement system. Thus isokinetic dynamometers can validly be used in subjects/patients that do not suffer from debilitating weakness (typically MMT grades 1, 2, 3) and produce data that allow clinicians to judge even subtle changes.
Finally, it should be emphasized that the cruder the resolution of the system, the chances of being more reproducible are higher. Thus if a tester is asked to rate the strength of muscles as either 4 or 5 (based on bilateral testing), it is likely that the reproducibility will be high. In other words if it is rated as 4, on retest and under the same conditions, it will remain 4. However, the ability to make any clinical interpretation from such a result is absolutely limited as grade 4 is particularly wide. If on the other hand the resolution is made higher e.g. one of the following: 3+, −4, 4, 4+, −5 then the clinical content is much higher but as the reproducibility is extremely low, there is little that can be inferred from such measurements.
HOW DO THESE CONCEPTS COME INTO THE DOMAIN OF CHANGE?
The basic tenet is that measurements of the same clinical entity differ from one test session to the other, when spanned over days or weeks. This is true for normal subjects and, especially, for patients. As mentioned above such a difference depends on the resolution of the measurement scale. This is the normal fluctuation taking place with respect to all biological parameters and in the relevant context. Suppose for example that stature (height) of an adult is measured by cm, standing upright and shod, and the result is 176 cm. It is highly likely that on a second test, one week later, the result will be the same. If however, the measurement is in mm, the first score of 1,763 mm may change to 1,765 mm a week later. Has the subject increased in height? Has there been a change?
Now, let us get back to the previous example where due to exercise rehabilitation, a patient with a reconstructed ACL increased his Lysholm score from 61 to 72 from week 6 to week 8 after the operation. Is this a clinically meaningful change? is it a significant change? is it a change at all? Another patient who suffered from shoulder pain due to subacromial bursitis scored 78 mm on the visual analogue scale (VAS) at the first visit to the therapist. Two weeks later his VAS score is down to 59 mm. Is this a clinically meaningful change?
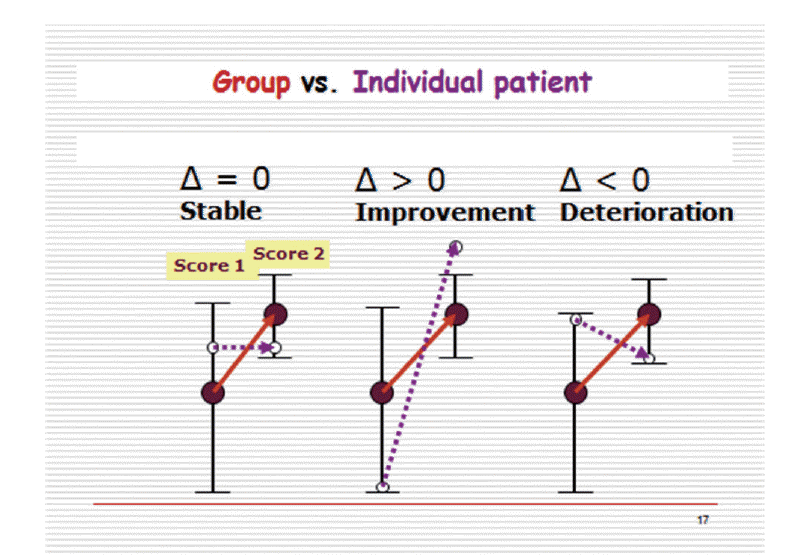
Before trying to answer these questions, the concepts of significant change vs clinically meaningful change have to be defined. Significant change is a group-based concept. Thus, if for instance a treatment method is assessed, and the design is based on an experimental, a control and a sham group, significant differences may be noted, for relevant outcome parameters on a within- and inter-group basis. This can lead to a conclusion that the method changes (improves) significantly the health status of the patient group. However it says nothing about the individual patient in the group which is best exemplified by Fig. 2.
In this example the mean value of a specific outcome measure of the group changes significantly to a higher level as indicated by the upward pointing solid arrow. On the other hand, 3 individuals who are included in this group, might not change (Δ=0), improve with the group, although not as drastically (Δ>0), or even deteriorate over the duration of the experiment (Δ<0). Therefore, whereas on the whole, the treatment is effective, at the level of the individual patient/subject this is not necessarily so. This leads one to the inevitable consequence that the term ‘significant change’ in the context of improvement or aggravation of a health status is misleading inasmuch as it relates to the individual. This contrasts with the main objective of clinical practice, that is, to improve the condition of the individual or at least not to cause any harm.
This conflict furnished the basis for the relatively new research field relating to the concept of change at the individual level. The research has initially focused on what is known as the error of measurement and its various descriptors, also known as clinimetric parameters. The term ‘smallest real difference’ (SRD), became increasingly applied and it related to some numerical value, the cutoff, that delineates what should be the clinically smallest meaningful change at the level of the individual from what is known as the ‘error of measurement’. It should be mentioned that these values may apply (with the necessary variations) to a group, but they are not used as often. The SRD is one of the mainstays of the Distribution Model which compares the change in a patient-reported outcome score to some measure of variability such as the SD, the effect size or the standard error of measurement (SEM).
The error of measurement which is the aggregate of factors that collectively blurs the true value of the measurement, serves as the main indicator for change. It is, in other words the ‘±’ around the difference. Included in the error of measurement are elements related to the measuring instruments, e.g. mechanical or electronic drift, the tester (high vs low skill), the patient/subject, the test protocol and the test environmental conditions. When weighted together, these factors result in the fact that the margins of uncertainty regarding an individual subject/patient are much wider than those acting for the group.
The SRD derives directly from the SEM (Lexell and Downham, 2005). In this context, the SEM is based on a test-retest study of a specific outcome measure. The correlation coefficient - Pearson’s r or ICC - is calculated along the common standard deviation (SD) and the SEM then derives from the following equation: SEM=SD√(1-ICC).
As can be seen, the SEM takes into account both the dispersion around the mean and the degree of correlation between the two measurements. Thus, if the test and retest scores perfectly overlap, the ICC is 1 and the SEM is 0. On the other hand if the ICC is 0, then the SEM is equal to the pooled SD. However, To derive the SRD, which is applicable to the individual subject/patient (heretofore SRDi), at a level of confidence of 95%, the SEM has to be multiplied by 1.96√2. Thus, according to the distribution model approach, the smallest real difference indicating change at the level of the individual subject or patient, is ±2.77 SEM. This fairly large margin accounts for the multitude of factors that can affect the real score. To indicate a clinically meaningful change at the group lever - SRDg - the cutoff is smaller and is equal to 1.96 SEM. Clearly, if a reproducibility study proves, that the test-retest correlation under strict experimental conditions is 1.0, then the SRD=0 (individual or group) which means that any difference in an outcome score is clinically meaningful. For instance if a patient reports an improvement of one point up on the Lysholm Scale, say from 66 to 67, this would be considered a clinically meaningful change. Obviously this is not the case, since perfect test-retest correlation based on a reasonable time interval (e.g. 1 w), in patients, is a practical impossibility. Moreover, even for the undiscerning eye, a difference of one point over a scale of 100 points, would be considered within the measurement error. On the other hand, how many points are needed to establish a clinically meaningful difference in terms of the SRD is something that cannot be estimated unless a proper reproducibility study is undertaken.
To further illuminate the use of the SRD for assessing individual change consider the following example in which a group of patients suffering from chronic cervical pain were assessed before and after the administration of a new exercise-based treatment for cervical pain. In order to find out who among the patients really benefitted from this treatment, namely exceeded the SRDi/improved meaningfully, and whether the group as a whole benefitted from the treatment, namely the group’s mean score was greater than the SRDg, a test-retest study was undertaken prior to the study in this group. The patients were asked to rate their cervical pain twice over a period of 1 week. The test-retest correlation was 0.72 while the pooled (test+retest) SD was 25 mm. The SRDi was therefore 2.77×25√(1–0.72) =37 mm whereas the SRDg was 26 mm. This means that only those patients who have lowered their VAS score by 37 mm or more underwent a clinically meaningful change. For instance a patient who has rated his VAS as 88 mm and 60 mm before and after treatment, respectively, did not undergo a clinically meaningful change as the difference |88-60| = 28 mm was less than the cutoff value. This would have been the same decision if the patient started with a VAS score of e.g. 62 mm and completed the protocol with a VAS of 28 mm. Furthermore, while in the previous case the improvement was by about 33%, in the latter it was by more than 50%, yet for both cases the result is the same: no meaningful clinical improvement. On the other hand if the group’s mean score before the exercise program was 88 mm and after it −60 mm -the difference was greater than 26 mm and therefore, the treatment was effective. Interestingly, for this group the ‘after-before’ difference in the VAS scores was highly significant (P<0.001) and still remained significant (P<0.05) even if the improvement was reduced to 20 mm. This underlines the profound difference between an analysis which is based on straightforward statistical tests of significance (e.g. ‘t-test’ for matched samples) and the SRDg approach which is more vigorous. Clearly, neither apply at the individual level.
The surprising result vis-à-vis the individual patient namely that even differences as high as 35 mm are not sufficient to judge a clinically meaningful change stems from the strict standards imposed by the modern understanding of the meaning of change. There is little doubt that with reasonable SDs, had a group of patients with neck pain improve by 50% or even 33%, such an improvement could qualify as significant, paving the way for the possible further application of the new protocol, subject to its relevancy. However, when the individual patient is concerned, the margin of error is much wider as ‘errors’ do not even out in the same way as they do for a group. Thus, in this case, even a dramatic improvement in the VAS may not qualify for a change. On the other hand, setting strict criteria, and applying them to the individual patient, allows e.g. a more focused look at the possible advantages and pitfalls of a specific treatment approach while enabling the clinician to apply the approach with more confidence.
What are the factors that take part in ‘stiffening’ the criteria for the SRD or other clinimetrics-oriented parameters? Looking at the SEM-based SRD formula, it is clear that two factors have a direct effect of the magnitude of the SRD: the SD and the ICC (r). Largely, increasing the sample size should reduce the SD and thus bring down the SRD. Equally, increasing the ICC will decrease the value of √(1-ICC) with the same effect. Both will make it ‘easier’ for the individual patient to exceed the SRDi and increase the rate of clinically meaningful ‘responders’ in the group. On the other hand, under the same conditions, the more homogenous the group, the lesser is the ICC (r). Thus, extreme cases (outliers) will push the ICC up but at the same time will make the group less homogenous, inevitably limiting the generalizations that may operate with respect to a certain intervention. Reproducibility studies that furnish the building stones for SRD analysis tend to include relatively small number of participants with the inevitable consequence that the SRD is relatively large leading to sometimes paradoxical results. One solution for this weakness is to increase the sample size as a larger N plays a decisive role in reducing the SD. In addition, sticking to well established protocols and using accurate and responsive instruments should further help in having a larger percentage of the participants cross the SRDi cutoff. It should be emphasized that the SRD is not the only parameter used for the analysis of change but certainly one of the most common.
As mentioned above, the distribution model is heavily based on reproducibility studies that quantify the error of measurement, enabling the separation of the true change from the ‘noise’ embedded in the outcome score. This is an objective approach that does not consider either the patient’s or the clinician’s subjective feeling/impression/judgment regarding the success, no effect or even failure of the intervention. This realization led to the application of an alternative approach to the issue of change, the so-called anchor-based approach. The mainstay of this approach is the Minimal Clinically Important Difference (MCID), a concept that differs quite sharply from the clinimetric SRD. The MCID has been defined in multiple ways but the most essential definition is probably the one by Jaeschke et al. (1989) which stipulates that it is the smallest difference in a score, in a domain of interest, that patients perceive as beneficial and that would mandate, in the absence of side-effects, a change in the patient’s management”. Another often quoted definition is by the American Thoracic Society (2007) “The smallest difference that clinicians and patients would care about”. According to this model, the change in a patient-reported outcome score is compared to some other measure of change - the anchor or the external criterion. Thus the objective error of measurement is essentially eliminated and replaced by a coupling of subjective and an objective measures. The MCID is also known by the terms Smallest Detectable Difference (SDD), Minimal Detectable Change (MDC) or Minimal Detectable Difference (MDD).
NUMERIC PAIN RATING SCALE
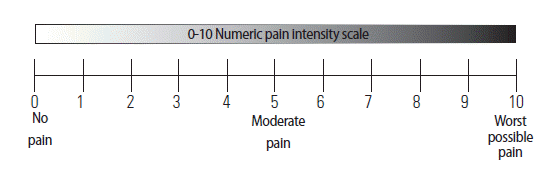
To demonstrate the specific qualities of this approach consider the study by Michener et al. (2011) where 136 patients presenting with shoulder pain were assessed twice, before and after 3–4 weeks of rehabilitation. Prior to treatment the patients filled the 11-point Numeric Pain Rating Scale (NRS, Fig. 3) a well-established tool for self-assessment of pain. They did so with respect to 3 conditions of pain: at rest, with normal daily activities, and with strenuous activities. The mean of these conditions was considered the representative score. Patients also filled the Penn Shoulder Score (PSS) which includes questions relating to pain (based on an 11 p scale), satisfaction (based on 7 categories scale), and function (based on 5-category scale and 20 questions). The relative weights of these sections were 30. Ten and Sixty, respectively, bringing the total score to 100 points (for a full view of the PSS see, http://www.eliterehabsolutions.com/pdfs/PENN%20SHOULDER%20SCORE.pdf.) Previous research has indicated that for the function scale, 8.6 points (about 15%) is the MCID for the function section namely, patients can be classified as meaningfully improved if their score is ≥8.6 point, or not improved, otherwise. Thus 8.6 points was used as an external criterion anchor. The MCID for the average NPRS for all patients was 2.17, for both the surgical and nonsurgical subgroup. This means that a change of slightly more than 2 points, around 20% of the full scale, is the smallest difference value associated with a clinically meaningful change.
Obviously with the existence of another parameter - the anchor – and an associated (MCID) begs the question why use the other one. The answer is the efficiency of using the latter and the relatively straightforward findings it provides. For example, although smaller MCIDs have been found, e.g. 1.3 on the 0–10 Numeric Pain Rating Scale (Cleland et al., 2008), the majority of studies looking at different disorders, have indicated that using similar scales for pain the typical MCID was 2 and above. Thus it could be argued that a meaningful improvement could roughly be traced when a decrease of about 20% in the rating of the pain was achieved. Another issue is the relationship between the MCID and the level of statistical significance when an intervention is applied. It is possible an MCID might be larger than the difference associated with statistical significance, especially a clinical trial involving a large population. Under such circumstances the ‘significant difference’ could be of little practical importance as the situation regarding the individual participant in such a study, or indeed a patient, is unclear. An opposite situation may also arise when clinicians believe they know fairly well what the MCID might look like, e.g. an improvement of 20° in knee RoM following some surgical intervention although the difference was not significant. Such case calls for careful application of the MCID. At any rate it should be understood that the MCID is instrument-dependent, where ‘instrument’ means most often a questionnaire of some sort. Moreover, although such questionnaires, that frequently refer to quality of life (QOL) or function, look quite similar, they are objective-dependent. Thus for example, a QOL questionnaire relating to problems with lower limb, should dwell particularly on ambulation whereas for the upper limb, an important issue would be manipulation of objects.
To sum up, judging the existence of change in rehabilitation is very complex. This situation is a result of the special type of assessment instruments, the role of the patient and the clinician in performing the test, and the fluctuating nature of some of the main outcome measures e.g. pain and function. As a result not every difference carries a clinical meaning. Moreover, even significant differences fail to tell whether a change occurs, unless the objective of the decision is the group. Thus, in order to judge the existence of change, in most cases due to intervention but occasionally as a natural resolution of the symptoms, specific approaches to the problem have to be used. The former model is based on reproducibility parameters such as the SEM and normally mandates large and homogenous samples whereas the latter is particularly suitable when functional measures are employed. The change parameters derived from these approaches are not identical in value and the decision which is more appropriate is context-dependent. Clearly, although much has yet to be done, our current understanding already permits a deeper insight into the fascinating problem of change.
CONCLUSIONS
Determination of change in the context of rehabilitation is an involved issue but that requires critical attention. Modern statistical methods combined with profound clinical reasoning may give the clinical community appropriate tools for deciding whether a change observed as a mere difference score is also a clinically meaningful one.